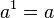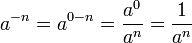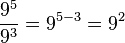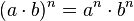EJEMPLOS Y EJERCICIOS

Su definición varía según el conjunto numérico al que pertenezca el exponente:

  • Cuando el exponente es un número natural, equivale a multiplicar un número por sí mismo varias veces: el exponente determina la cantidad de veces.
a^n = \underbrace{a \times \cdots \times a}_n,

Por ejemplo: 2^4 = 2 \cdot 2 \cdot 2 \cdot 2 = 16 .

  • Cuando el exponente es un número entero negativo, equivale a la fracción inversa de la base pero con exponente positivo.
a^{-p}= \frac{1}{a^p}
  • Cuando el exponente es una fracción irreducible n/m, equivale a una raíz:
a^{\frac{n}{m}} = \sqrt[m]{a^n}

Cualquier número elevado a el exponente 0 el resultado equivale a 1, excepto el caso particular de 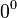0^0\, que, en principio, no está definido (ver cero).

La definición de potenciación puede extenderse a exponentes reales, complejos o incluso matriciales.

Potencia de exponente 0

Un número elevado al exponente 0 da como resultado la unidad (1), puesto que:

1 = \frac {a^n} {a^n} = a^{n-n} = a^0\,

Potencia de exponente 1

Toda potencia de exponente 1 es igual a la base:

a^1 = a \,

Ejemplo:

54^1=54 \,

Potencia de exponente negativo

Un número elevado a un exponente negativo, es igual al inverso de la misma expresión pero con exponente positivo:

a^{-n} = a^{0-n} = \frac {a^0}{a^n} = \frac {1}{a^n}\,

 Multiplicación de potencias de igual base

El producto de dos o más potencias de igual base es igual a la base elevada a la suma de los correspondientes exponentes (se escribe la misma base y se suman los exponentes):

a^m \cdot a^n = a^{m + n}

Ejemplos:

9^3 \cdot 9^2 = 9^{3+2}= 9^5

 División de potencias de igual base

La división de dos potencias de igual base es igual a la base elevada a la resta de los exponentes respectivos:

\frac{a^m}{a^n} = a^{m - n}

Ejemplo:

\frac{9^5}{9^3} = 9^{5-3}= 9^2

 Potencia de un producto

La potencia de un producto es igual al producto de los factores elevados cada uno al exponente de dicha potencia. Es decir, una potencia de base a.b y de exponente n, es igual al factor a elevado a n, multiplicado por el factor b también elevado a n:

(a \cdot b)^n=a^n \cdot b^n

 Potencia de una potencia